En realidad no es tan dificil, de hacer, son unas cuantas lineas de codigo, el problema es entender los fundamentos de la integracion y derivacion numerica.
Dime que tan preciso necesitas que sea? Para la integracion numerica, para que no te lo compliques tanto con la regla de 3/8 de simpson (que a mi gusto es de las mas precisas), puedes utilizar rectangulos.
Veras, la integracion de una funcion, no es nada mas que encontrar el area bajo la grafica de una funcion. (El area bajo la curva)
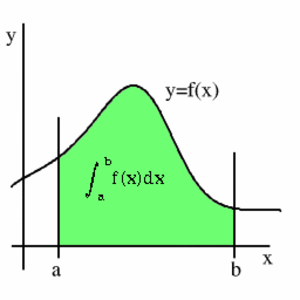
Pero esto que significa exactamente? Veras, todas las funciones polinomiales te generan una grafica, y si encuentras el area bajo la grafica de una determinada funcion, entonces estas encontrando la integral numerica de dicha funcion.
Si lo que buscas no es necesariamente precision, puedes utilizar el metodo de los rectangulos para encontrar la integral numerica.
El metodo de los rectangulos basicamente consiste en que, vas a ver la grafica como si estuviera hecha a base de puros rectangulos, posteriormente encuentras el area de cada rectangulo, y lo vas sumando hasta que sumes el area de todos los rectangulos detro del intervalo [a,b].
Observa la siguiente grafica:

Veras que la grafica esta dividida en rectangulos, si encuentras el area de cada rectangulo y despues la sumas, estas encontrando el area bajo la curva.
Como veras, en la grafica, hay una h en la parte baja, y representa el espaciado que hay entre punto y punto. Este espaciado te sirve para encontrar la precision de tus resultados. En el primer escenario, con una h grande (un espaciado grande), veras que hay muchos errores de sobre estimacion, y sub estimacion, lo cual repercute directa y negativamente en la exactitud y validez de tu resultado.
Si disminuyes el espaciado, disminuyes a su vez el error, lo cual te da una mejor precision, aunque no te fies demasiado, que este metodo no es de los mas correctos que existen. Es para el programador "flojo" o poco precavido, o que realmente no le interesa la exactitud del resultado.
En este caso, la base del rectangulo, es el valor de h, y la altura del rectangulo, va a ser la evaluacion de la funcion a integrar, en cada uno de los puntos sobre el eje de las X.
Ya en cuestion de programacion, necesitas tener un vector, con los intervalos en el eje de las X.
Por ejemplo, si quieres encontrar la integral de la funcion x en el intervalo [0,1] con un espaciado H = 0.1
Entonces necesitas crear un vector con los valores
[
0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,
1]
Donde el primer y ultimo numero del vector, son los limites de la integral.
digamos que el vector lo llamamos A
Entonces, la integral de la funcion X, la encontrarias de la siguiente manera:
Integral += evalua(mifuncion,A[i]) * H;
donde la funcion evalua, va a evaluar, el numero en la posicion A[i] con cualquiera que sea el valor de mifuncion.
ahora, si no te quieres meter en lios de evaluacion simbolica, tu funcion tambien la puedes guardar en un vector, y utilizas asignacion dinamica de memoria, para tener una funciona polinomial de orden N
Este es un ejemplo de funcion polinomial:
10x^3 + 8x^2 - 34x + 2
Las reglas matematicas dicen que las funciones se deben escribir de mayor a menor exponente y con una constante (un numero) al final, si el numero es diferente de cero.
Entonces podemos generalizar la regla de la siguiente manera:
ax^n + ax^(n-1) + ax^(n-2) + ...+ ax^(n-k) + ax + C
donde C representa una constante.
Entonces puedes almacenar las funciones polinomiales en un vector, especificando que tienen que ser escritas correctamente.
Por ejemplo si quisieran escribir la funcion x^2 + 3x + 2
Tendrias que pedir un vector con los valores
[1 , 3 , 2] y pedir el orden la funcion, en este caso es de orden 2, y ya con eso podrias aplicar la generalizacion de la formula, y evaluar tu funcion en cualquier punto.
Si quisieras escribir la funcion x^5 + 1, entonces tu vector tiene la forma:
[1 0 0 0 0 1]
Lo que estas escribiendo son los coeficientes, la computadora te entenderia algo como:
1x^5 + 0x^4 + 0 x^3 + 0x^2 + 0x + 1
Si quisieras representar la funcion 5x3 + 40, el vector quedaria:
[5 0 0 40]
Tiene sentido?
Te quedaria algo parecido a:
Código C++:
Ver originalfuncion = [1, 3, 2];
orden = 2;
k=0;
Resultado = 0;
/*Evaluando un numero en el punto 0.1*/
for(int i = 0; i < orden; i++)
{
Resultado
+= funcion
[i
]*pow(0.1,orden
-k
);k = (k!=orden)?k+1;
}
Resultado += funcion[orden];
No te fies del codigo de arriba, son las 3 AM aca y ando medio dormido :) pero mas o menos seria asi, para evaluar una funcion polinomial en un punto determinado, lo unico seria reemplazar el 0.1, por el valor del vector que te puse anteriormente con el espaciado, ya con eso tendrias una integral numerica, mas o menos correcta.





