La 1era es esta aclaración, la 2nda es la clave y la 3era es info extra a quien requiera o le interese.
Además en gris puse lo menos importante.
--------------------------------------------------------------------------------------------
El juego es así:
1- Se genera un número al azar de 3 cifras usando números enteros del 0 al 5, sin repetir. Yo no sé el número que se genera (a menos que haga trampa, pero no quiero).
2- Yo elijo un número de dichas condiciones (excepto el ser por azar).
3- El juego informa cuántos números bien colocados (considerando el número elegido por la computadora) puse, y cuántos números están mal colocados.
El paso 2 y 3 se repiten hasta digamos decir 6 códigos fallidos o hasta que yo acierte el número elegido por la compu.
Cuando digo hacer fuerza bruta me refiero a hacer un "programa" (lo digo entre comillas porque más de uno dice que yo no programo, que hago otra cosa) que encuentre las mejores respuestas o algo que luego un humano pueda usar para ganar rápido en el juego, digamos procesos a seguir. Y que además dicho "programa" sea lo más fácil posible de hacer sin importar lo poco eficiente que sea. Pero que además esté hecho en un lenguaje "normal", no en lenguaje máquina.
Bueno, yo hice algunas cosas así, pero esto la verdad me sobrepasa por el tema de las pistas creo (entiendo que es muy vago decirlo así, pero no lo entiendo más que eso), por ahora no sé hacerlo, por eso hago este tema para pedir ayuda.
Lo que hice hace años fue algo así:
Hay un objeto en el punto 0 del eje de las X.
El objetivo es que llegue al 10 en la menor cantidad de movimientos posibles teniendo estos 2:
1: Moverse +1 a la derecha (hacia el 10).
2: Moverse -1 a la izquierda.
Es obvio que conviene usar la acción 1 10 veces, pero mi idea era que el programa lo descubriera sin que yo le diera pistas como "te estás acercando", no me gusta hacer eso porque uno no siempre sabe cuando una acción es buena o mala, prefiero evaluar "desde el final". Mi programa realizaba una acción, si llegaba a una situación nueva generaba un archivo cuyo nombre la describía y el contenido marcaba cual fue la anterior y qué hizo en ella, y se generaba otro archivo que marcaba que esa situación aún no había sido analizada. Tras probar todas las acciones en una situación (reseteándola luego de cada una), se hacía lo mismo pero desde una de esas situaciones no analizadas. El resultado básicamente son archivos así:
1.txt que tiene X=0; Action=1
2.txt que tiene X=1; Action=1
3.txt que tiene X=2; Action=1
etc, hasta
10.txt que tiene X=9; Action=1
Y por supuesto los otros archivos de situaciones por acciones estúpidas como -1.txt por haberse movido hacia atrás.
Cuando el programa llegaba a colocar el objeto en el punto 10, decía la acción que realizó, cargaba la situación anterior, decía la acción que se realizó en ella, y así sucesivamente hasta llegar a la situación inicial.
Eso me parece que es aplicable a "todo":
Hacer un jaque mate, hallar la cura a una enfermedad o a un país mal gobernado, etc.
Si no se puede es porque hay variables desconocidas por ejemplo, pero quizá el mismo método con los ajustes necesarios las puede averiguar, al fin y al cabo es un método para averiguar cosas.
En este foro me plantearon un problema del que sin embargo no podía: Hacer la serie de fibonacci con alguna condición que no creo venga al caso. Quizá no pude porque no lo apliqué bien, pero tampoco creo que venga mucho al caso, aunque por decir algo...:
Si se genera una serie a comprobar si sirve o no, necesito la serie verdadera para hacer esa comprobación. Si no sé cómo es ("variable desonocida") no puedo hacer la comprobación, y si sé cómo es y la voy a usar para hacer comprobaciones entonces qué sentido tiene buscarla.
Es un caso distinto de lo que yo plantee, en que se puede saber qué se quiere pero no cómo conseguirlo, saber el final de una serie pero no la serie en sí que además es irrelevante (pueden ser cualquier números, simplemente dependen de las acciones/situaciones posibles). Sólo porque un número esté bien ya tengo "la serie" (los movimientos para llegar a dicho número), pero en el caso de la serie de fibonacci es necesario que estén bien todos sus números y si no tengo la serie (o no la genero a propósito) no puedo. En fin, no tengo mucha idea de eso (quizá hay una ecuación matemática para saber si un número está en la serie, aunque no se tenga la serie, pero ni idea tampoco, no sé hallar condiciones o efectos aún, sólo hallé series de números basados en el último principalmente).
Y aquí estoy de nuevo con un problema que ese método supuestamente "todo terreno" no sé cómo puede solucionar esto, y si es que no puede, por qué no.
¿Cual sería el método más parecido al mío, que solucionaría el problema?
¿Cómo deben ser los archivos?
Se me ocurre por ejemplo esto:
012,00_345,03_453,03_534.txt
El nombre contiene las acciones realizadas y las pistas recibidas (el contenido en sí del archivo no se me ocurre). ¿pero cómo se generaría eso?
¿Cual es la situación inicial, debo mencionar el número que yo en teoría no conozco? El resultado sería este:
Para el 012 conviene usar 012
Para el 013 conviene usar 013
Inútil.
Necesito que se generen los procesos y contar la cantidad de pasos que requieren en cada caso, o al menos la máxima cantidad de pasos que requiere en un caso.
¿Esos procesos no se pueden describir mediante una línea?
Pero a ver, por ejemplo me serviría que exista un archivo
012,01_304,01_135,02_253,01_541.txt
y otro:
012,01_304,02etc.txt
Suponiendo que iniciar con 012 y luego 304 (si la pista es 01) fuese uno de los procesos que mejor funciona en general. O sea, no necesito que un proceso con todas sus variaciones esté en 1 línea, pueden ser muchas líneas/archivos indicando las diferentes variaciones según las pistas.
Luego de algún modo buscaría los archivos más cortos, de hecho podría ponerles LX al inicio y sustituir X por la cantidad de números que tienen luego.
Entonces si jugando al juego pongo 012 y obtengo 11 busco el proceso 012,11, veo qué dice después, y así sucesivamente.
Algo que se me ocurrió es generar un proceso, que puede ser 012,013,014etc, y contar en todos los casos cuánto tardaría en averiguarlos. Es decir, ignora las pistas. ¿Será esa la respuesta? No creo, sin pistas cualquier proceso puede tardar mucho.
¿Pistas en los nombres de archivos y acciones dentro? No sabría bien cómo contar qué tarda más. Podría eliminar los archivos más largos y ver cual proceso se repite más ¿?
Creo que esto no serviría, iguales pistas pueden obtenerse por distintas situaciones, los archivos serían sustituidos por otros.
Af. dado un número N el proceso P1 tarda 1 paso.
No, tampoco, porque cuando digo proceso me refiero a una línea y si me basara sólo en los que tardan menos obtendría los que por suerte aciertan de una.
En fin, como ven le doy vueltas pero no me sale.
--------------------------------------------------------------------------------------------
MasterMind:
https://es.wikipedia.org/wiki/Mastermind
Más info aquí:
https://en.wikipedia.org/wiki/Master...me)#Algorithms
Ejemplo del juego que dije:
1- Se genera el número 210
2.1- Digo 012
3.1- Me dice 1-2, lo cual significa que hay 1 número bien colocado (el 1, pero yo eso en realidad no puedo saberlo en este punto porque en el caso real no sé el número generado) y 2 mal colocados.
2.2- Debido a que en este caso habría tenido bastante suerte porque acerté cuales números son los presentes, sólo me queda averiguar el orden correcto. Sé que el número es alguno de estos 3: 021, 210 o 102. A partir de ahora es cuestión de probar esos 3, no sé si hay un orden de pruebas mejor que otro.
Búsqueda de modos de ganar antes de hacer este tema:
Quería tener un diagrama de flujo o algo similar:
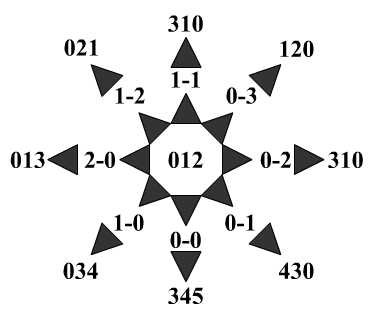
Dado que habría muchas flechas en cada caso, pensé en hacer algo así:
012__0-0__345__0-3__453__0-3__534
_______________1-2__354__0-3__435__0-3__543
_____0-1
Por otro lado, pensando una explicación para un ejemplo en que me equivoqué, se me ocurrió un método que no me interesa usar en programación pero es interesante:
En cada columna de la siguiente "tabla" están los posibles números de cada cifra:
000
111
222
333
444
555
La mayoría de las posibles pistas nos permiten tachar algunos números.
El ejemplo siempre será 012.
0-1 o 0-2:
_00
1_1
22_
333
444
555
0-3:
_00
1_1
22_
___
___
___
1-0 o 2-0:
0__
_1_
__2
333
444
555
0-0:
___
___
___
333
444
555
1-2:
000
111
222
___
___
___
1-1:
Creo que esta no.



