Comenzando a programar: 6c - Condiciones booleanas y selección simple.

[Kyshuo]

Veamos las tablas de verdad:



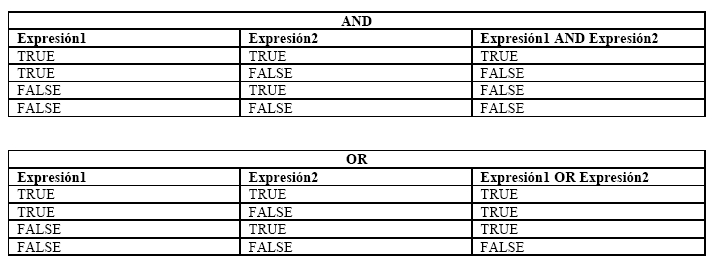
Existe también el operador booleano NOT que niega una condición, o sea, da el valor opuesto a esta. En principio uno se pregunta para que serviría algo como eso. Más adelante cuando comencemos a trabajar con las variables boolean veremos el uso de este operador. Veamos su tabla:




Operadores relacionales: Son los que comparan dos expresiones, tal y como hemos venido haciendo hasta ahora:




Un ejemplo matemático:

Bien. Haremos un programa en el cual aplicaremos casi todo lo dado hasta ahora.
Se nos pide realizar un programa que calcule las raíces de polinomios de segundo grado cuyos coeficientes serán ingresados por el usuario, y muestre en pantalla los mensajes correspondientes.

Por si alguno de ustedes no está bien familiarizado con polinomios explicaré brevemente lo que es uno de segundo grado:
Un polinomio es una función matemática con una única incógnita X la cual está elevada a distintos exponentes en los diferentes términos de la ecuación. Para que se vea mejor, un polinomio de segundo grado tiene la forma

aX^2 + bX + c

donde a, b y c son números reales. Por ejemplo, un polinomio podría ser 2X^2 + 4X + 2. Los números que acompañan a las X (a, b y c) son llamados coeficientes.

Las raíces de un polinomio son aquellos valores de X que hacen que la ecuación sea nula, o sea, que valga 0.
En el ejemplo que tenemos allí, una raíz de ese polinomio es -1. Si cambiamos la incógnita X por -1 efectivamente vemos que todo se anula:

2*(-1)^2 + 4*(-1) + 2 = 2*1 – 4 + 2 = 2 – 4 + 2= -2 + 2 = 0.

Dado un polinomio de segundo grado puede suceder que tenga dos raíces diferentes, una única raíz (llamada raíz doble) o que no tenga raíz. Para hallar las raíces de un polinomio aX^2 + bX + c se usa la conocida fórmula de Bascaras:



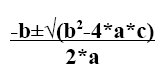
El término bajo la raíz cuadrada (b^2-4*a*c) es llamado discriminante ya que de él depende si el polinomio tiene dos raíces, una sola o no tiene. Si el discriminante es mayor que 0 efectivamente tendremos dos raíces distintas ya que por la forma de la fórmula tenemos un ± que divide la fórmula en dos partes, por un lado resolvemos la ecuación con el signo de + luego de –b, y después resolvemos la fórmula con el signo de – luego del –b:



Esto dará dos resultados diferentes, cada uno correspondiendo a una raíz.
Si el discriminante es nulo, o sea igual a 0, la raíz cuadrada de 0 es igual a 0, por tanto sería estúpido separar en dos la ecuación ya que hacer –b+0 o –b-0 da exactamente igual, por lo cual el resultado será único. En este caso tenemos una única raíz doble.

Si el discriminante es menor que 0 no podremos hallar su raíz cuadrada ya que no existe raíz de un número negativo. En este caso la fórmula no puede resolverse y decimos que no existen raíces reales. En este caso pueden hallarse raíces complejas, pero eso no lo haremos ahora ya que tiene sentido solo para aquellos que se lleven bien con las matemáticas.

Muy bien, teniendo cierto conocimiento sobre el problema comencemos a plantearnos como lo resolveremos para programarlo. El usuario ingresará en la entrada estándar los coeficientes a, b y c de nuestro polinomio. Teniendo esos valores primero debemos verificar que el valor a sea distinto de 0 ya que de ser así no estaríamos enfrentándonos a un polinomio de segundo grado sino a uno de grado uno o cero. Además, por la forma de la fórmula de Bascaras, si a vale 0 entonces 2*a también, y esté término es el divisor; al no poder dividir por 0 estaríamos enfrentándonos aun problema.

Luego deberemos evaluar el discriminante y según lo que este dé cómo resultado tomaremos tres caminos distintos para mostrar los resultados al usuario.

He aquí el código:

Código Pascal:

PROGRAM polinomio;
 
Var
    a, b, c: real; //Los coeficientes del polinomio.
    discriminante: real; //El discriminante.
    raiz1, raiz2: real; //Las raíces del polinomio.
 
BEGIN
     //Pedimos al usuario el ingreso de datos y leemos los mismos.
    write('Ingrese los coeficientes separados por espacio: ');
    readln(a,b,c);
 
    //Verificamos que el coeficiente a sea no nulo.
    If a=0 then
       writeln('Usted no ha ingresado un polinomio de segundo grado.')
    else
    begin
       //Calculamos el discriminante.
       discriminante:= sqr(b)-4*a*c;
 
       //Tomaremos los tres caminos según el valor discriminante.
       If discriminante=0 then
       begin
           //El polinomio tiene una única raíz.
           raiz1:= -b/(2*a);
           writeln('El polinomio tiene una raíz doble: ',raiz1:2:2);
       end
       else
           If discriminante>0 then
           begin
              //El polinomio tiene dos raíces.
              raiz1:=(-b+sqrt(discriminante))/(2*a);
              raiz2:=(-b-sqrt(discriminante))/(2*a);
 
              writeln('El polinomio tiene dos raíces reales: ',raiz1:2:2,' y ',raiz2:2:2);
          end
          else
              writeln('No existen raíces reales.');
     end; //Fin de la instrucción ELSE del IF principal.
END.
 

Muy bien, como primera cosa les diré que a pesar de la explicación que yo pueda dar aquí será conveniente que ustedes mismos estudien este programa para comprenderlo bien. No es para nada complicado pero puede resultar confuso gracias a las anidaciones que se han hecho de las funciones IF…THEN…ELSE.

En las líneas 4, 5 y 6 declaramos todas las variables necesarias para que nuestro programa funcione correctamente. En la línea número 11 leemos los tres coeficientes a la vez. Luego tenemos un IF…THEN…ELSE principal que, si el coeficiente a es igual a 0 mostrará un mensaje de error al usuario y solo en caso contrario pasará a realizar todas las demás tareas en su instrucción ELSE, la cual es un enorme bloque de instrucciones encerradas entre begin y end. En ese caso calculamos primero el discriminante ya que de él dependerán los caminos a tomar. Observar que al hacerlo (en la línea 19) usamos la función sqr que calcula el cuadrado de un número. En vez de eso podríamos haber puesto b*b que es lo mismo.

Si el discriminante es igual a 0 mostraremos al usuario la raíz doble, sino, si el discriminante es mayor que 0 calculamos y mostramos ambas raíces, y en caso contrario le diremos al usuario que no existen raíces reales.
Es importante que entiendan el uso de los begin y end en este programa. Recuerden que estos delimitan bloques de programa los cuales son vistos como una única instrucción. Si escribiera el código anterior a partir del primer IF de modo que en cada sentencia tuviéramos una única instrucción quedaría así:

Código Pascal:

If condicion1 then
   Instruccion1
Else
Begin
   //Aquí debería estar el cálculo del discriminante.
   If condicion2 then
      Instruccion2
   Else
      If condicion3 then
         Instruccion3
      Else
         Instruccion4;
End;
 

Esto, si tomáramos todo lo que está entre el BEGIN y el END que vemos allí como una única instrucción quedaría simplemente como

Código Pascal:

If condicion1 then
   Instruccion1
Else
   Instruccion2;
 

donde la Instruccion2 sería todo el enorme bloque entre el BEGIN y END.

-------------------------------------------------------------------------------------

Continuamos en la parte d. Esto de que solo se permitan 10.000 caracteres me limita muchísimo, pero bueno, al menos se puede leer