Ejercicios:
Ejercicio2: Modifiquen los programas anteriores para que, si el usuario no ingresa un entero, notifiquen el error y vuelvan a pedir el valor correcto.
-----------------------------------------------------------------
Ejercicio3: Se llama matriz cuadrada a toda aquella matriz que tiene tantas filas como columnas, o sea, si tiene 5 filas tiene 5 columnas. La transpuesta de una matriz cuadrada es aquella matriz que tiene como columnas lo que antes eran filas. O sea, si tenemos una matriz cuadrada A, una matriz cuadrada B es transpuesta de A si las columnas de B son iguales a las filas de A, o sea, si se satisface que B[i,j]=A[j,i] para todos los valores posibles de i y j.
Ejemplo. Sea A de 5 filas y 5 columnas como se muestra en la figura, veamos como sería su transpuesta B:
A
1 2 3 4 5
0 0 0 0 0
1 1 1 1 1
5 4 3 2 1
2 2 2 2 2
B
1 0 1 5 2
2 0 1 4 2
3 0 1 3 2
4 0 1 2 2
5 0 1 1 2
Como ven, lo que en A eran filas, en B son columnas. La primera fila de A que contiene los valores 1, 2, 3, 4 y 5 es la primera columna de B 1, 2, 3, 4 y 5, y así sucesivamente.
Escriban un programa que calcule la transpuesta de un arreglo de números reales con cinco renglones y cinco columnas. Los valores de la matriz se leen desde la entrada estándar. El resultado se debe imprimir en la salida estándar. Recuerden la relación B[i,j]=A[j,i] para que sean transpuestas.
Este ejercicio no es muy complicado. Tal vez lo peor de esto es que trabaja con una propiedad matemática de las matrices y para aquellos que no lo han estudiado puede resultar difícil de comprender. Aún así creo que no deberían tener problemas, sin embargo se trata de comprender el Álgebra Lineal y eso no es lo que quiero en este curso.
-------------------------------------------------------------------------------------
Arreglos tridimensionales:
Esto es básicamente lo mismo. Se declaran exactamente igual solo que ahora habrá tres subrangos entre paréntesis rectos y por ende deberemos colocar tres coordenadas para indicar cual celda deseamos ver (una coordenada para la fila (altura), otra para la columna (largo) y otra para el eje (ancho)). Hago esta aclaración porque si bien un arreglo bidimensional dibuja una tabla, uno tridimensional dibuja un prisma y por tanto debemos decir cuan a lo alto, largo y ancho queremos posicionarnos.
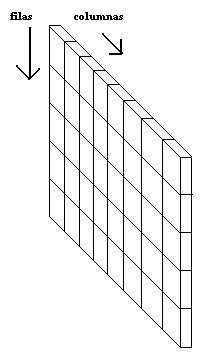
Esto es un arreglo bidimensional de 5 filas y 8 columnas. Visto de este modo es un rectángulo donde la cantidad de filas son su altura y la cantidad de columnas su largo. Este es un arreglo de 5x8.
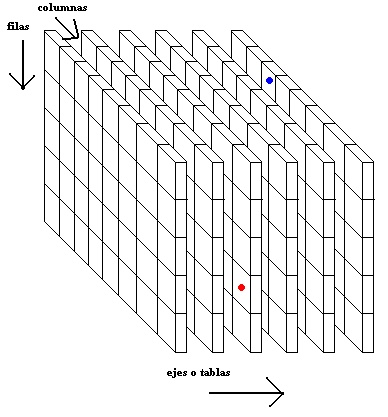
Así podríamos visualizar un arreglo tridimensional de 5x8x6. Como ven es un arreglo de tablas que estarían todas bien pegadas formando un prisma. Nosotros debemos indicar en qué fila y columna está nuestra celda y en cual tabla de todas. Siempre indicamos [fila, columna, tabla]. Esto es un intento de que puedan visualizar un arreglo tridimensional.
El punto rojo correspondería a la posición [4,8,3] por estar en la cuarta fila, octava columna de la tercera tabla. El azul correspondería a la posición [1,3,6]. Hasta aquí llegamos con arreglos, en la siguiente lección les propondré un proyecto llamado Master Mind enfocado para el uso de arreglos, pero necesito que me comenten que tal la llevan hasta ahora, qué les parece todo y si creen que vale la pena continuar de esta manera.
-------------------------------------------------------------------------------------
Librería CRT:
Limpiar la pantalla: Muchas veces puede resultar muy conveniente el hecho de borrar el contenido de la pantalla para mostrar uno nuevo y no que lo anterior se desplace hacia arriba. Ustedes mismos habrán visto que al ejecutar mediante el IDE varias veces un programa, todo lo que se muestra en la pantalla va quedando allí, lo cual hace que se vea feo o confuso en varios casos.
Para lograr limpiar la pantalla utilizaremos una librería de pascal. Esto no se corresponde con el cometido de este curso por lo que solo explicaré cómo limpiar la pantalla. El uso de librerías lo veremos más adelante cuando abordemos la programación en Modula 2; si no manejan bien todos los conceptos que hay aquí pues simplemente no tiene sentido seguir con cosas más complejas.
¿Qué es una librería? Básicamente es una unidad de programa que consta de funciones y procedimientos (lo veremos más adelante) que alguien programó y puso a nuestra disposición para que podamos utilizarlos. Dicho de manera sencilla para que se entienda ahora, una librería consta de un código fuente ya compilado pero que no crea un archivo .exe, sino que queda en otro formato. La librería tiene un nombre y además, dentro de su código tiene "partes" que nosotros podemos llamar y utilizar para nuestros propósitos. Para usar una librería simplemente debemos saber su nombre y claro, qué partes de ella queremos usar.
Existen librerías por defecto que ya vienen con el compilador, pero hay otras que pueden obtenerse por la web.
Existe una librería incluida en Free Pascal llamada CRT. Esta librería nos provee de funciones para el control de la pantalla y el teclado. De todas ellas solo nos interesa una, ClrScr, lo cual es una abreviación de Clear Screen, que significa Limpiar Pantalla.
Para indicar las librerías que vamos a usar debemos escribir la palabra
reservada USES luego de la declaración del identificador de nuestro programa. Luego de USES escribimos los nombres de nuestras librerías y ya, podemos comenzar llamar a sus funciones y procedimientos sin problema. Veamos un simple ejemplo de la limpieza de la pantalla:
Código Pascal:
Este programa lo único que hace es dibujar un cuadro de 20x20 utilizando el carácter #, luego borra el dibujo y muestra un nuevo mensaje. El procedimiento clrscr puede ser llamado cada vez que queramos.Ver original
En resumen, escriben USES crt antes de declarar constantes, tipos y variables, y luego pueden usar clrscr en cualquier parte de su programa para borrar todo su contenido.
Saludos.



