Dado que casi nadie ha hecho preguntas ni ha comentado nada, asumo que la llevan bien con la lección anterior y pues, publico esta como anexo ya que es un poco más de lo mismo. Espero que comenten en esta lección como llevan el curso hasta ahora, qué les ha parecido las explicaciones dadas, si creen que se entiende bien a pesar de la complejidad creciente, etc. De verdad eso es un estímulo para continuar con este trabajo.
Los arreglos que hemos visto hasta ahora son unidimensionales (lineales), o sea, de una única dimensión. Se dice esto ya que se requiere una única coordenada (índice) para ubicar una celda del mismo. Sin embargo es posible definir arreglos de dos dimensiones (2D), de tres dimensiones (3D) y más. Aquí veremos ejemplos de arreglos de hasta tres dimensiones ya que no requerimos de más para trabajar, sin embargo muchos programas usan arreglos de N dimensiones. Como nosotros existimos en un espacio de dimensión 3 solo podemos ver gráficamente arreglos de dimensión 3 o menor, pero visualizar un arreglo de dimensión 4 o más se hace difícil y no compete a este curso.
Arreglos bidimensionales:
Comencemos por ver arreglos de dos dimensiones. Estos dibujarán una tabla de datos del mismo tipo, también conocidas matemáticamente como matrices.
Hay dos maneras de declarar arreglos bidimensionales, una es declarar un arreglo de un arreglo, o sea, un arreglo cuyas celdas sean también arreglos. Esta es la forma más fea de hacerlo y la que menos recomiendo, pero existe. Veámoslo en un ejemplo:
Código Pascal:
Ver original
En la línea 4 vemos un tipo arr1 que es un arreglo de 5 celdas de enteros. En la línea 5 vemos el tipo Tabla que es un arreglo de 7 celdas del tipo arr1, o sea que cada celda es un arreglo de 5 celdas. Si dibujáramos Tabla al igual que lo hicimos antes tendríamos 7 celdas del 1 al 7, esto estaría indicando cuantas filas tiene nuestra tabla. Si desplegamos cada celda de Tabla estaríamos abriendo hacia la derecha 5 lugares con lo cual estaríamos indicando las columnas de nuestra tabla.
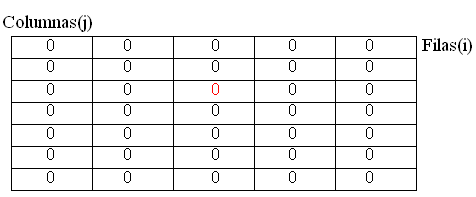
Ese sería el dibujo de Tabla, como ven hay 7 filas (líneas horizontales) y 5 columnas (líneas verticales). El 0 corresponde a la posición (3,3) de la tabla ya que está en la fila 3 y en la columna 3. Siempre para una tabla se especificarán las coordenadas de una celda nombrando primero el número de filas y luego el de columnas.
En la línea 9 del ejemplo declaramos la variable matriz del tipo Tabla. El trabajo con los arreglos bidimensionales es idéntico al de los arreglos unidimensionales. Cada celda es una variable independiente y para acceder a cada una simplemente nombramos nuestro arreglo y damos entre paréntesis rectos las coordenadas de nuestra celda separadas por comas. La forma genérica sería así:
Variable_arreglo[fila,columna]
de este modo, si quisiéramos ir a la celda que está en la fila 7 y en la columna 4 deberíamos escribir matriz[7,4].
En nuestro programa de ejemplo asignamos a cada celda el valor 0. Como ven debemos usar dos FOR anidados para recorrer una tabla, uno para recorrer las filas y otro para las columnas.
Vean que el subrango en arr1 indica cuántas columnas tendrá la matriz y en subrango en Tabla indica cuántas filas.
Una sintaxis alterna para acceder a una celda de nuestra tabla es la siguiente:
Variable_arreglo[fila][columna]
y por tanto si, usando esta sintaxis, quisiéramos acceder a la fila 7 y la columna 4 deberíamos escribir matriz[7][4]. No recomiendo esta sintaxis.
Veamos ahora la segunda forma de declarar un arreglo bidimensional, la cual es la que yo recomiendo que usen:
Código Pascal:
Ver original
Como ven en la línea 4 hemos declarado el tipo Tabla en el cual hemos incluido dos subrangos entre los paréntesis rectos separados por coma. El primer subrango (1..7) indica la cantidad de filas y el segundo (1..5) la cantidad de columnas que tendrá la matriz. Esto siempre es así. Como ven, de este modo queda todo mucho más claro.
NOTA: La cantidad de celdas de un arreglo bidimensional es igual al resultado de multiplicar la cantidad de filas por la cantidad de columnas.
Como ejercicio quiero que modifiquen ese programa para que despliegue en la salida estándar la matriz. En este caso aparecerá una tabla de 0 como esta:
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
Esto no es muy difícil y radica explícitamente en el uso de FOR.
Continuamos en la parte b...



